「99%の投資家は小さく勝って大きく負けてしまう…」その一歩先へ！＝田渕直也

効用曲線と損失回避バイアス

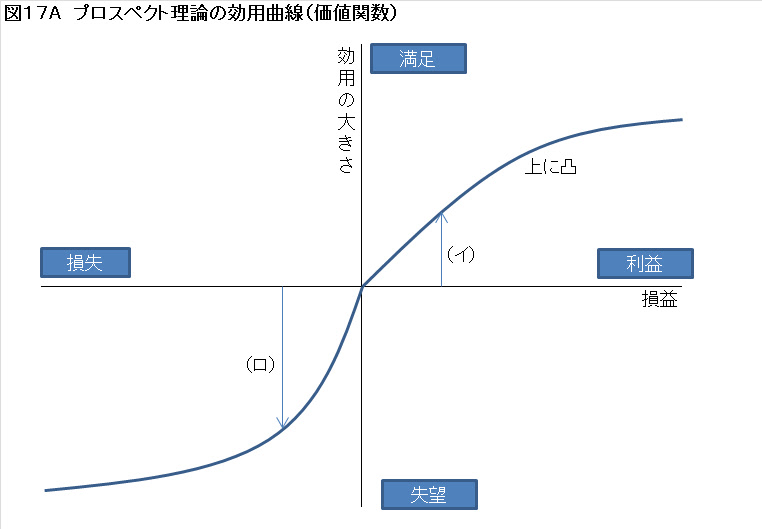
プロスペクト理論では、利益や損失に対する心理的な満足度、すなわち効用の度合いを関数として表します。これが図17Aです。

一方で、利益や損失がどの程度の確率で発生すると感じているかという主観的な確率も関数として表します（図17B）。

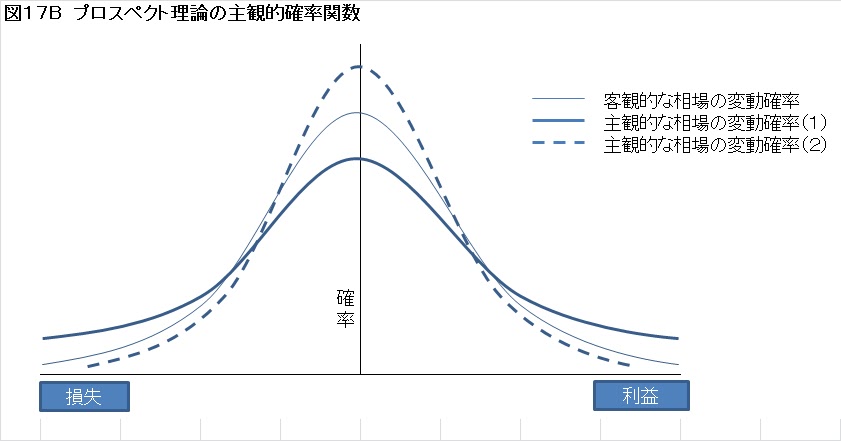
この二つの関数を掛け合わせた結果として、意思決定が行われると考えるわけです。

もう少し具体的に見てみましょう。まずは効用関数からです。

効用関数（価値関数ともいう）は、利益を評価する右半分のエリアでは、上に凸となる曲線で表されています。これは、利益の増加に伴って満足度の増加が少しずつ小さくなっていくことを示しています。限界的な効用が逓減しているわけですね。

一方で、損失を評価する左半分のエリアでは、効用曲線は下に凸となる曲線で表されます。これは、損失の増加に対してマイナスの満足度、すなわち失望の増加の度合いが小さくなっていくことを示しています。

先ほどの質問では、確率が明示されていたので、主観的確率関数の影響がなく、効用関数だけで意思決定がなされることになります。その場合、AとBの選択では、利益に対する満足度の比較となりますから、

10万円の利益の満足度　＞　50％×0　＋　50％×20万円の利益の満足度

となって、選択肢のAが選ばれます。同様に、損失に対する失望度の比較では、

10万円の損失の失望度　＞　50％×0　＋　50％×20万円の損失の失望度

となって、失望の度合いが小さい選択肢Dが選ばれることになります。

このプロスペクト理論の効用曲線にはもう一つ重要な特徴があります。それは、X軸の中心のゼロのところで、効用曲線が屈折している点です。

これは、50％の確率で10万円を受け取り、50％の確率で10万円を支払うゲームを人がどの程度好むかを表しています。一般に、人はこのようなフィフティ・フィフティのゲームを好みません。つまり、同額の利益から得られる満足度よりも、損失から生じる失望度の大きさの方が大きいというわけです。これは図17Aでは

（ロ）の大きさ　＞　（イ）の大きさ

で表されています。そうだとすると、人は損失を回避しようとするバイアスを持っていることになります。

もっとも、このような効用曲線の性質は、人によって、もっと厳密にいうと人が置かれた状況によって、異なってくると考えられます。

たとえば、トレードで失敗して損失を被った後では、損失回避傾向は強く現れますが、成功が続くとこれが弱まっていきます。効用曲線は、固定的なものではなく、状況に応じて変動していると考えるべきものなのです。

Next: 人は「めったに起きないが印象的な出来事」の発生確率を高く見積もる